
TEMA 4 : Funciones
Apartado 4.2.2
Tablas y gráficos
A partir de la fórmula podemos construir una tabla de valores.
Dando valores a la variable independiente X obtenemos su correspondiente valor de la variable dependiente Y
Ejemplo 1
Obtener cinco puntos de la función y=f(x)=5*x-3 y representarla gráficamente
Vamos a darle los siguiente valores a la x, (variable independiente)
x = 0 -> y = 5*0 - 3 = -3
x = 1 -> y = 5*1 - 3 = 2
x = 2 -> y = 5*2 - 3 = 7
x =-1 -> y = 5*(-1) - 3 = -8
x =-2 -> y = 5*(-2) - 3 = -13
Tabla

Representación gráfica
Cuando x = 0 y = -3 , obtenemos el par (0,-3)
Cuando x = 1 y = 2 , obtenemos el par (1,2)
Cuando x = 2 y = 7 , obtenemos el par (2,7)
Cuando x = -1 y = -8 , obtenemos el par (-1,-8)
Cuando x = -2 y = -13 , obtenemos el par (-2,-13)
Situamos los puntos en el plano cartesiano y los unimos con una línea que pase por todos ellos.

Ejemplo 2
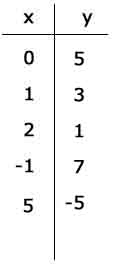
a) dada la función f(x)=-2x+5 escribe una tabla de cinco valores y representa esos puntos en el plano
x = 0 -> y = (-2)*0 + 5 = 5
x = 1 -> y = (-2)*1 + 5 = 3
x = 2 -> y = (-2)*2 + 5 = 1
x =-1 -> y = (-2)*(-1) + 5 = 7
x = 5 -> y = (-2)*5 + 5 = -5
b) obtén la representación gráfica de la función
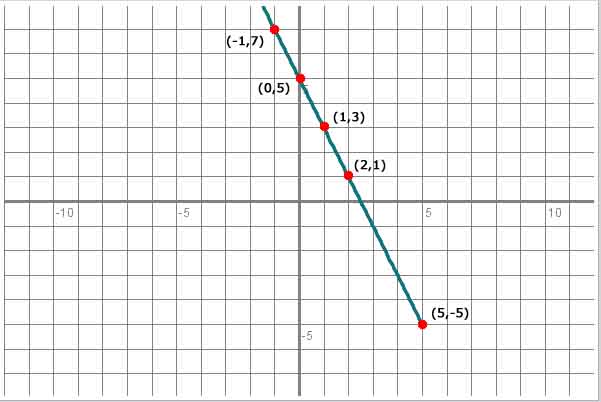
Cuando x = 0 y = 5 , obtenemos el par (0,5)
Cuando x = 1 y = 3 , obtenemos el par (1,3)
Cuando x = 2 y = 1 , obtenemos el par (2,1)
Cuando x = -1 y = 7 , obtenemos el par (-1,7)
Cuando x = 5 y = -5 , obtenemos el par (5,-5)
Si trazamos una recta por todos los puntos obtenemos su representación grágica
c) ¿ El par (3,4) es de la función y=f(x)=-2x+5 ?
Si x = 3 -> y=f(x)=-2(3)+5 = -6 + 5 = -1 ≠ 4 , por tanto el par (3,4) NO es de la función