TEMA 4 : Funciones
Apartado 4.1
Coordenadas cartesianas
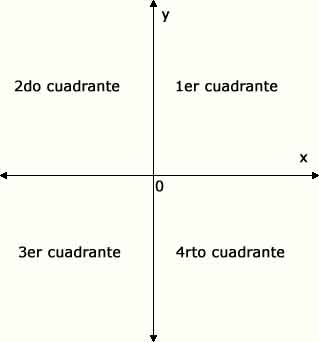
1.Sistema de coordenadas cartesianas
Vamos a representar puntos en el plano.
Para ello utilizaremos el sistema de coordenadas cartesianas que está formado por dos rectas perpendiculares que se cortan en un punto., 0, llamado origen de las coordenadas.

La recta horizontal se representa por X y se llama eje de abcisas.
La recta vertical se representa por Y y se llama eje de ordenadas.
Cualquier punto P del plano queda determinado por un par de números (x,y) llamados coordenadas cartesianas del punto P y se escriben P(x,y) : . x se llama abcisa del punto P y permite desplazar el punto P hacia la derecha (si x es positivo) ó hacia la izquierda (si x es negativo). y se llama ordenada del punto P y permite desplazar el punto P hacia arriba (si y es positivo) ó hacia abajo (si y es negativo).
Ejemplos
a) Vamos a representar los puntos (2,3) , (-2,3) y (0,0) en el plano
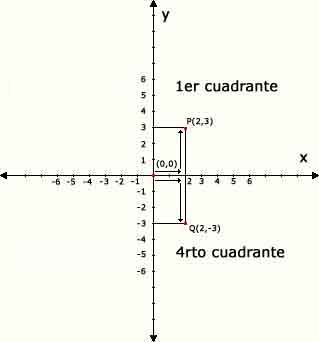
P(2,3) -> x=2 y =3 -> 2 > 0 (+) desplazamos a la derecha , 3 > 0 (+) desplazamos arriba
Q(2,-3) -> x=2 y =-3 -> 2 > 0 (+) desplazamos a la derecha , 3 < 0 (-) desplazamos abajo
O(0,0) -> x=0 y =0 -> El punto O(0,0) es el origen de coordenadas cartesianas
b) Vamos a representar los puntos (-4,2) y (-4,-2) en el plano
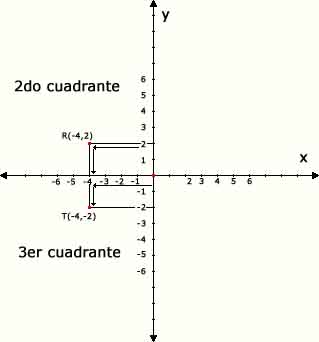
R(-4,2) -> x=-4 y =2 -> -4 < 0 (-) desplazamos a la izquierda , 2 > 0 (+) desplazamos arriba
T(-4,-2) -> x=-4 y =-2 -> -4 < 0 (-) desplazamos a la izquierda , -2 < 0 (-) desplazamos abajo
2.Puntos especiales
Son aquellos puntos donde o la componente x = 0 o la componente y = 0
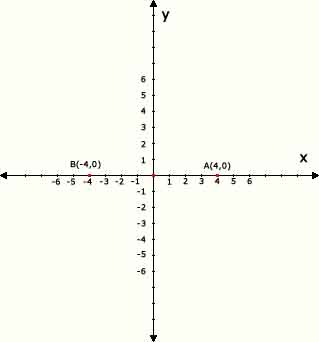
a) Puntos del tipo (a,0) ( cuando y = 0 )
A(4,0) -> x=4 y =0 -> 4 > 0 (+) desplazamos a la derecha , 0 = 0 ni sube ni baja
B(-4,0) -> x=-4 y =0 -> -4 < 0 (-) desplazamos a la izquierda , 0 = 0 ni sube ni baja
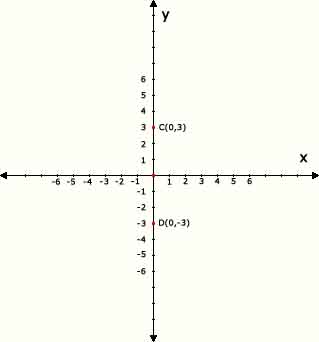
b) Puntos del tipo (0,b) ( cuando x = 0 )
C(0,3) -> x=0 y =3 -> 0 = 0 ni derecha ni izquierda , 3 > 0 (+) desplazamos arriba
D(0,-3) -> x=0 y =-3 -> 0 = 0 ni derecha ni izquierda , -3 < 0 (-) desplazamos abajo