TEMA 3 : Teorema de Pitágoras
Apartado 3.2.2
Aplicaciones
a) Un triángulo será rectángulo si verifica el teorema de
Pitágoras.Si no lo verifica, entonces, no será rectángulo.
Ejemplos
a1) Comprueba si el triángulo de lados 6,8,10 es rectángulo
10 = hipotenusa, por ser el mayor
6,8 = catetos
a = 10, b = 6, c = 8
a2 = b2 + c2 -> 102 = 62 + 82 -> 100 = 64 + 36 -> 100 = 100 , verifica Pitágoras , es un triángulo rectángulo.
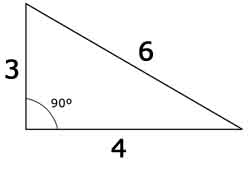
a2) ¿Es rectángulo el siguiente triángulo?

a = 6 = hipotenusa por ser el mayor
b= 4, c = 3 catetos
a2 = b2 + c2 -> 62 = 32 + 42 -> 36 = 9 + 16 -> 36 ≠ 25 , NO es cierto -> NO verifica Pitágoras -> NO es un rectángulo
b) Cálculo de la hipotenusa conociendo los dos catetos
hipotenusa = √[ (cateto)2 + (cateto)2]
Ejemplos
b1) Calcula la diagonal de un rectángulo de lados 9 y 12 centímetros
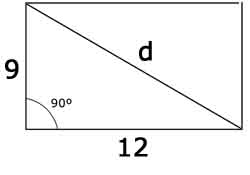
Estamos
calculando la hipotenusa de un triángulo rectángulo de catetos 9 y 12
centímetros.
Por lo tanto :
a
= d
b = 9, c = 12
a2 = b2 + c2 -> d2 = 81 + 144 -> d =√(225) = 15 centímetros
b2) Calcula el lado de un rombo de diagonales D = 16 y d = 12 centímetros
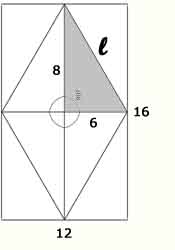
Estamos
calculando la hipotenusa de un triángulo rectángulo de catetos 6 y 8
centímetros.
Por lo tanto :
a
= l
b = 6, c = 8
a2 = b2 + c2 -> l 2 = 36 + 64 -> l =√(100) = 10 centímetros
c) Cálculo de un cateto conociendo la hipotenusa y otro cateto
cateto1 = √[ (hipotenusa)2 - (cateto2)2]
Ejemplos
c1) Altura de un triángulo isósceles de lados 10, 10 y 6 centímetros
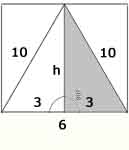
Estamos
calculando el cateto de un triángulo rectángulo de hipotenusa 10 y otro cateto
de 3 centímetros.
Por lo tanto :
a
= 10
b = h , c = 3
b = √(a2 - c2) -> h = √(100 - 9) -> h = √(91) -> 8,54 centímetros
c2) Apotema de un hexágono regular de lado 12 centímetros
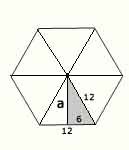
Estamos
calculando el cateto de un triángulo rectángulo de hipotenusa 12 y otro cateto
de 6 centímetros.
Por lo tanto :
a
= 12
b = a , c = 6
b = √(a2 - c2) -> a = √(144 - 36) -> h = √(108) -> 10,39 centímetros